Para entender de la forma más fácil posible qué intenta la Econometría y sin que caigamos en conceptos abstractos como “Método de los Mínimos Cuadrados” de frentón, se debe partir con un ejemplo.
Utilicemos los mismos datos de la entrada 1 de este Blog/Curso: Tenemos 10 alumnos con sus respectivas horas de estudio y calificaciones obtenidas. Resulta lo natural, que a mayor cantidad de horas tiende a haber calificaciones más altas, pero con excepciones. Sabemos que hay una relación, pero no es exacta, y también hay resultados variables entre las distintas personas, porque los alumnos son personas con capacidades y talentos distintos y no necesariamente el que más estudie obtendrá la mejor calificación, y lo mismo en el caso inverso. Recordemos los datos y grafiquemos la tabla utilizando el software R:
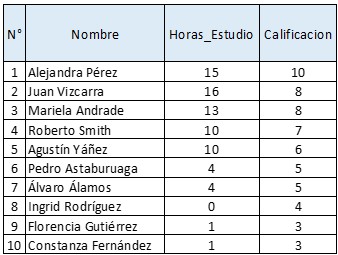
Antes de iniciar, te dejo el Excel aquí para que repliques los cálculos futuros:
Graficando en R (punto a tratar en futuras publicaciones), vemos que hay una especie de “línea recta” factible -recordar, que por convención en el eje horizontal va la variable independiente y en el eje vertical la variable dependiente, la que buscamos explicar, en este caso las calificaciones-. Podemos imaginar una línea que “mejor estima” los datos o que “es la más exacta para explicar los datos”, ya que, en cierta forma, al graficar los puntos estos pareciera que, si hacemos “zoom out” o alejamos la vista, se forma una línea recta que muestra la correlación positiva entre horas de estudio y calificación obtenida, es decir, la línea de tendencia:
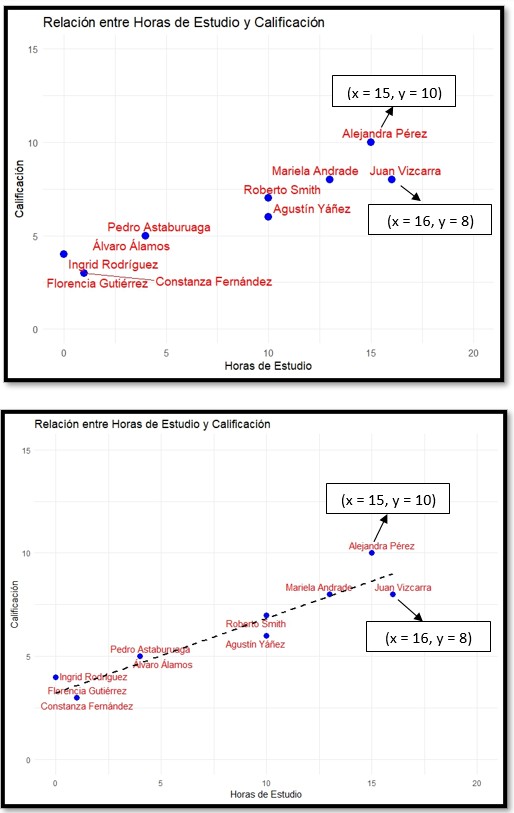
Ambas imágenes son la misma, solamente que la segunda incluye la línea de tendencia, la llamada Regresión Lineal que buscamos estimar.
¿Cómo logramos obtener esa Ecuación de la Recta (Regresión Lineal)?
Sabemos, por la publicación anterior, que la ecuación de una recta debe tener la siguiente forma:
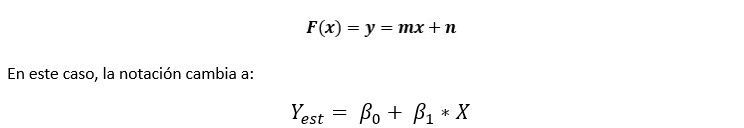
Se ha utilizado el subíndice “est” para indicar que es una estimación. Lo más fácil es iniciar, en base a los datos, con la estimación del «Beta sub 1» . Si te preguntas de dónde provienen las siguientes fórmulas, algo complicadas de entender a simple vista: De los matemáticos Karl Pearson (1857 – 1936) su explicación de forma rigurosa y de Legendre (1752 – 1833) / Gauss (1777 – 1855) su desarrollo previo en paralelo. No deja de se curiosa la inteligencia de Gauss, ya que desarrolló el método para predecir la órbita de los planetas… no para estimar una recta sin finalidad alguna. Por el momento, iremos a lo deseado y no en explicar cómo se llegó a esta fórmula. No dejan de ser las demostraciones la razón por la cual muchos estudiantes terminan odiando econometría. Entonces:
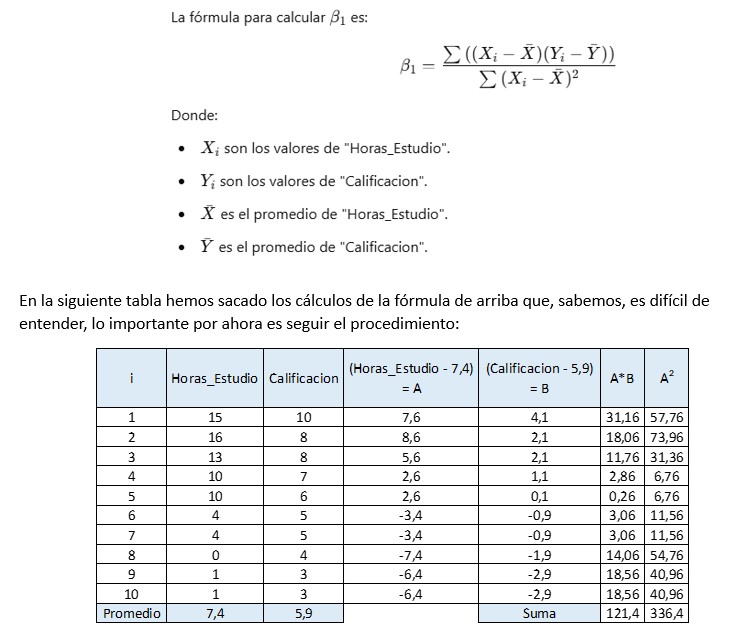

Esta es la “Ecuación de la Recta” que minimiza el error y por lo tanto, la línea de tendencia más exacta. Los gráficos fueron dibujados con el software R y los cálculos si vieron fueron hechos manualmente en Excel (se adjunta) para el paso a paso, esto se puede resolver con programación en R de manera fácil. Lo que veremos será lo siguiente:
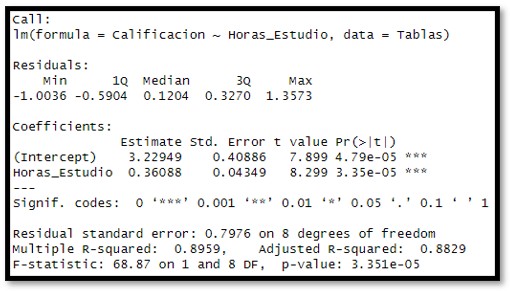
En próximas entradas al Blog veremos como realizarlo en R y como evaluar la calidad del ajuste de la regresión lineal a los datos.