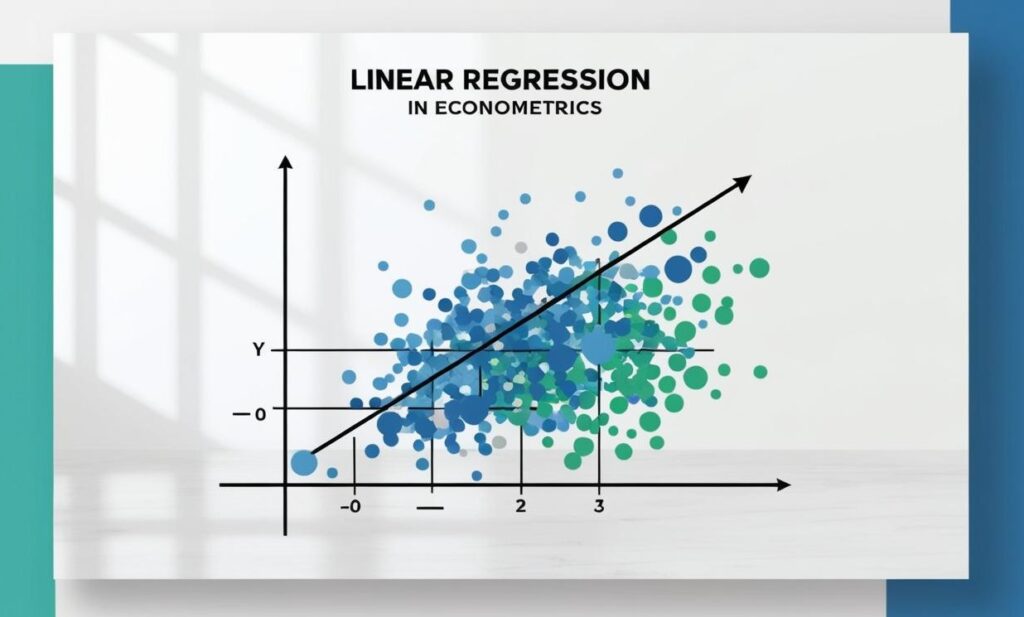
Como revisamos en la entrada anterior del blog -aunque no es necesario que la hayas visto si quieres saber qué es la ecuación de la recta-, la Econometría básica y más simple, busca estimar una recta que mejor explique los datos de los cuales se alimenta. No importa si no entiendes esta última frase, ya que es contenido que no hemos visto de momento. Vayamos por parte:
1) Concepto de Función Matemática
Una función matemática, en su definición más sencilla, es un proceso sobre el cual un número recibe una serie de cálculos sucesivos, dando como resultado otro número. El número de ingreso se suele denotar como “x” y el número resultante como “y” o “F(x)”. F(x) significa sencillamente algo como “El número resultante en función de “x””. Por esto mismo, se suele denotar F(x) = y.
Supongamos la función:

2) Plano Cartesiano
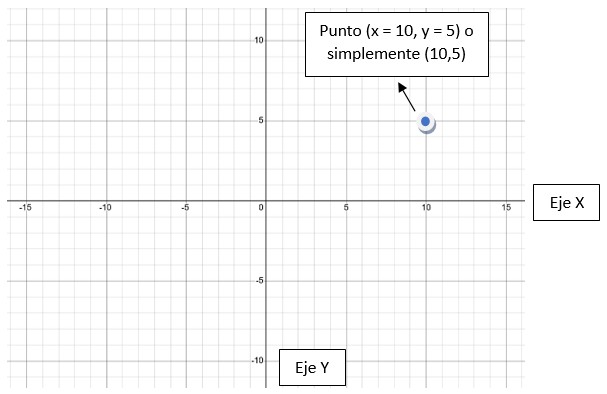
Un Plano Cartesiano corresponde a dos ejes, llamados X (horizontal) e Y (vertical). En estos ejes se enumeran los números negativos y positivos, por ejemplo, en la imagen inferior el eje X vemos del -15 al 15 y en el eje Y vemos escritos desde el -10 al 10 (por simplicidad, sólo se muestran los números cada 5 números naturales; por supuesto que cada cuadro equivale a un cuadrado de lado 1).
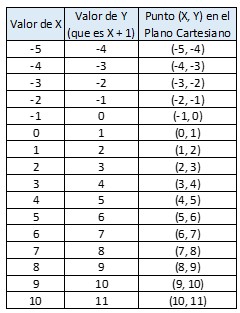
Por lo tanto, una función a la cual le ingresa un número X y devuelve como resultado un número Y, de la forma que vimos y = x + 1, estará compuesta por los siguientes números (estamos tomando números al azar):
Si esta recta la dibujamos en el Plano Cartesiano resultaría la línea roja. Se han marcado 3 puntos al azar:
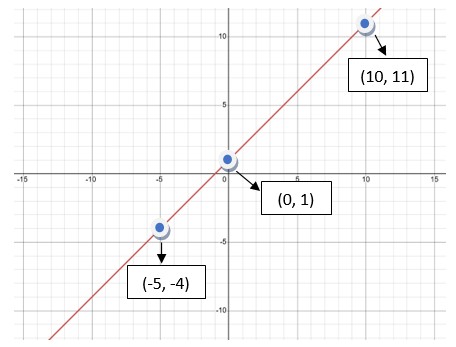
En síntesis, aquí vimos como una función al ser representada gráficamente se convirtió en una recta.
3) Ecuación de la recta que pasa por dos puntos en el Plano Cartesiano
Para seguir manteniendo la simplicidad de la explicación y no entrar en conceptos relacionados a la geometría, debemos entender que cualquier línea recta en el plano cartesiano se puede representar de la siguiente forma:
Los números “m” y “n” con dos números cualquiera. Como es obvio, “m” está multiplicando al número “x” que ingresa y “n” se suma posteriormente. Si te preguntas en qué se parece al ejemplo anterior es que era un ejemplo más sencillo:
En palabras: El valor de “m” era 1 y el valor de “n” también era 1. Por eso, por ejemplo, al ingresar un 5, éste quedaba igual (se multiplicaba por 1) y luego se le sumaba 1.
Ahora, la pregunta importante es: Si tengo dos puntos en plano cartesiano, ¿cómo puedo obtener la ecuación de la recta que me permite obtener todos los puntos?.
La respuesta es sencilla, y como se indicó, no se demostrará geométricamente, ya que nos enfocaremos sólo en lo práctico:
El valor de “n” es la diferencia de las “y”, y el valor del “n” lo puedes obtener despejando la ecuación resultante. Veamos el siguiente ejemplo:


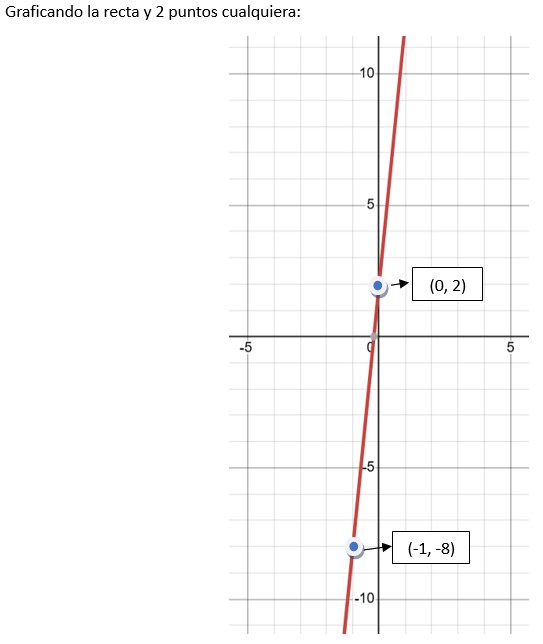
4) Conclusión:
La importancia de la Ecuación de la Recta radica en que mediante el método de “Estimación de Regresión Lineal Simple”, intentamos estimar la recta mediante un conjunto de puntos que se nos da, pero que no se comportan necesariamente formando una línea.
Lo que resultará, es la recta que mejor “estima”, es decir, la que minimiza los errores de estimación en el gráfico. ¡Esto será explicado en la próxima publicación del Blog!.