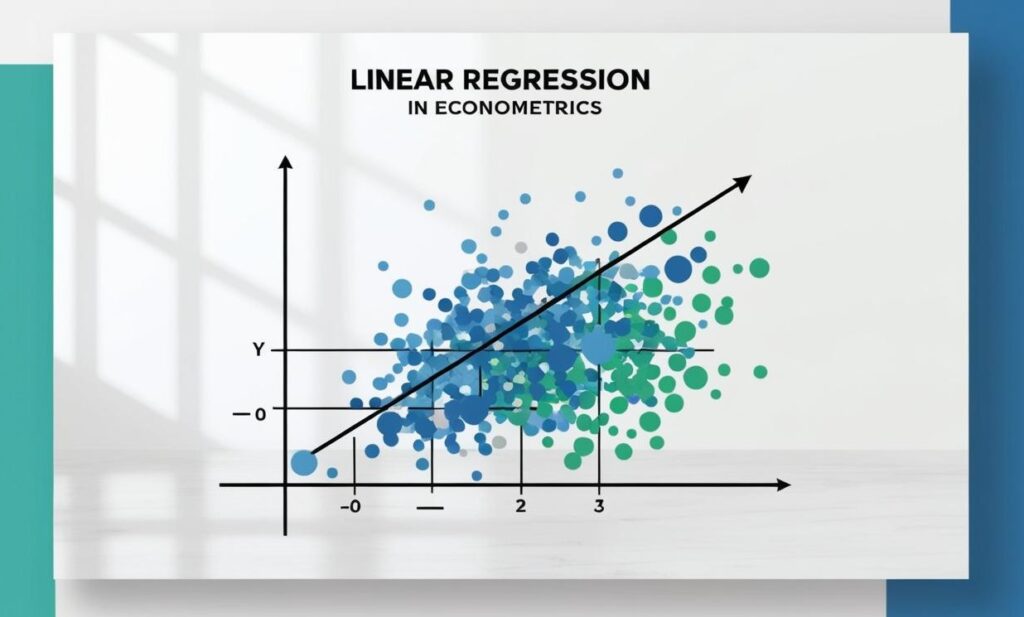
Como indica el capítulo 2 del clásico “Introducción a la Econometría” de Jeffrey M. Wooldridge: “Para realizar un trabajo empírico exitoso, es mucho más importante tener la capacidad de interpretar los coeficientes (nota: se refiere a las betas estimadas) que tener destreza para calcular fórmulas como la siguiente (indica este gráfico, que vimos en la entrada 3)”:
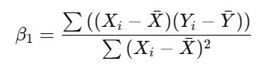
Dicho esto, parece conveniente aclarar conceptos que también, como se ha dicho, generan cierta animadversión al estudiante de Econometría. Veamos por parte todos estos conceptos. Primero, debes saber que el modelo de estimar las betas y, por lo tanto, la regresión lineal, se llama Modelo de Mínimos Cuadrados Ordinarios.
¿Qué es el modelo de Mínimos Cuadrados Ordinarios y por qué se llama así?
Se llama de Mínimos Cuadrados Ordinarios (MCO) porque utiliza un criterio muy específico para estimar los parámetros (betas o coeficientes) de la recta de regresión: minimizar la suma de los cuadrados de los errores (residuos) entre los valores observados y los valores predichos por el modelo. Errores o residuos se utiliza como sinónimo de la distancia de la recta. Es una forma análoga de decir lo que siempre buscamos: estimar la recta que mejor se ajusta a los datos.
Veamos qué significa esto, paso a paso, sin rodeos, pero con algo de elegancia matemática:
¿Qué intenta hacer el modelo de regresión?
Reiteremos: Busca ajustar una línea recta a un conjunto de puntos (datos) de manera que explique lo mejor posible la relación entre la variable dependiente “Y” y una o más variables independientes “X” (por el momento sólo hemos visto una X explicativa).
Hasta ahora no lo hemos visto, pero ya sabemos que la regresión de horas de estudio-calificación obtenida resultó ser:
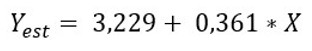
Pero los datos originales eran estos:
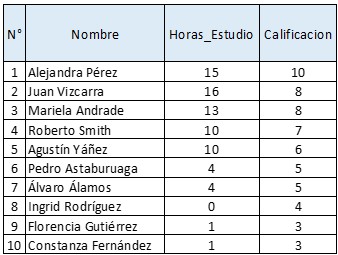
Veamos para Juan Vizcarra y sus X = 16 horas de estudio:
Sin embargo, el obtuvo una Y = Calificación = 8, por lo tanto, (8 – 9) = -1 es su error de estimación -recordar que el error de estimación es lo real menos lo estimado). En otras palabras, su ecuación específica real, corresponde a:
La forma genérica de escribir esto es:
Para cada alumno se debería agregar el subíndice “i” al lado de cada variable y al lado de las betas, pero en El Econometrista somos aversos a las complicaciones innecesarias. Se entiende que cada alumno tiene una ecuación similar con distintos valores. Al minimizar los errores, el nombre queda explicado. De forma indirecta, cabe agregar, que hemos minimizado la suma de los cuadrados de esos errores para estimar la recta de regresión lineal simple, como hicimos en la clase 3.
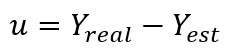
¿Por qué al cuadrado? Para:
- Evitar que los errores positivos y negativos se cancelen (se reitera que esto lo hicimos de forma indirecta. No importa, como tal, que no lo entiendas en simbología porque es una abstracción matemática. Pero sí lo puedes entender siguiendo las fórmulas del Excel que adjuntaré nuevamente aquí).
- Penalizar más los errores grandes (por ejemplo, un error de 10 pesa mucho más que uno de 2).
¿Y por qué «Ordinarios»?
Porque hay variantes más sofisticadas, como:
- Mínimos Cuadrados Generalizados (MCG),
- Mínimos Cuadrados Ponderados (MCP),
- o métodos robustos.
El «ordinario» señala que estamos usando:
- Errores con varianza constante (homocedasticidad),
- No hay autocorrelación entre errores,
- Linealidad en los parámetros, y
- Los errores tienen media cero.
Arriba se han utilizado varias palabras/conceptos que te explicamos a continuación.
El Teorema de Gauss-Markov
El teorema de Gauss-Markov establece que si se cumplen 5 condiciones, los estimadores (betas) de la regresión que hemos estimado son los mejores. Los hemos estado ocupando involuntariamente en todos los cálculos que hemos realizado, sólo que sin ser conscientes de ello, ya que van “dentro” de las fórmulas que se han presentado.
1 - Relación Lineal
El supuesto es que la relación entre la variable que intentas explicar y la/s variable/s explicativa/s es lineal.
Ejemplo: Si estudias 1 hora más, tu calificación aumenta de forma proporcional (por ejemplo, por cada hora adicional, subes 0,361 puntos en tu calificación, según nuestro ejemplo). Esto significa que si estudias 3 horas más, subirías 0,361*3 = 1,083 puntos, manteniendo una relación constante y predecible.
Contraejemplo: Si estudiar una hora adicional al principio mejora mucho tu calificación (por ejemplo, subes 5 puntos por esa primera hora), pero al añadir más horas, el efecto disminuye (estudiar 5 horas adicionales solo mejora 1 punto), entonces la relación no sería lineal. En el gráfico no veríamos una recta, sino que otra figura (de hecho, es posible que la relación REAL sea una especie de línea recta cuya pendiente empieza a aplanarse, ya que dedicar muchas horas al estudio hará que finalmente cada hora aporte menos al aprendizaje; ya solamente estás repasando lo que sabes).
Acá tienes un ejemplo de función no lineal (vemos que a cada aumento en X se reduce el aumento en Y, como si estudiáramos demasiado):
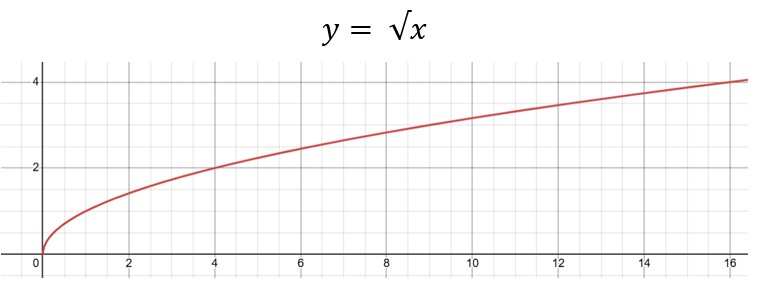
2 - Independencia de los Errores
Los errores (la diferencia entre lo que el modelo predice y lo que realmente sucede) deben ser independientes entre sí.
Ejemplo: Si predices las calificaciones de diferentes estudiantes basándote en sus horas de estudio, el error que cometas al predecir la calificación de un estudiante no debería influir en los errores de otros estudiantes. Si te equivocas mucho con un estudiante que estudió 5 horas, no implica que también te equivoques mucho con otro estudiante que estudió 7 horas. Si parece algo confuso, vamos al contraejemplo.
Contraejemplo: Si estás prediciendo las calificaciones de un grupo de estudiantes que estudiaron juntos o tienen métodos de estudio similares, los errores podrían estar relacionados. Si subestimas la calificación de uno, es probable que también subestimes la calificación de los demás, porque todos siguen un patrón común. Esto significa que el error en el planteamiento de la ecuación es que estarías midiendo las horas de un método de estudio en específico mezcladas con personas que tienen otro método o ningún método en específico, sólo su estilo personal. Para mejorar la condición, tendrías que agregar la variable predictiva “método de estudio”, pero las regresiones con múltiples variables explicativas todavía no las hemos revisado.
En general, si hay una dependencia de los errores a nivel de individuo (como que, si subestimas la nota en la prueba 1, en la 3 y en la 4… esto te llevará a sospechar que la 5 también estará subestimada. Acá puedes estar dejando fuera una variable como la motivación al estudiar) es porque hay un efecto individual no capturado.
4 - Esperanza (Valor Esperado) de los Errores es igual a Cero
En promedio, los errores del modelo deberían sumar cero.
Ejemplo: Si haces predicciones sobre las calificaciones de varios estudiantes, algunas veces el modelo subestimará las calificaciones y otras veces las sobreestimará. En promedio, estos errores deberían cancelarse y sumar cero. No debería haber un sesgo hacia calificaciones más altas o más bajas.
Contraejemplo: Si el modelo sistemáticamente subestima las calificaciones de los estudiantes que estudian poco y sobreestima las calificaciones de los que estudian mucho, entonces hay un sesgo, y los errores no sumarían cero en promedio.
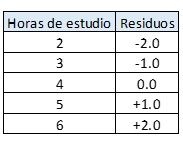
Esto no se comentó previamente, pero fue realizado en el cálculo, si te fijas en nuestra tabla de datos la suma de residuos da cero. Eso significa que el método de estimación de las betas estuvo bien aplicado:

Una nota importante y que revisaremos más adelante, es que esto se debe cumplir para cada valor de X en las regresiones lineales múltiples (con más de una X explicativa). En esencia la fórmula general es:
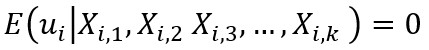
Esto significa que el error no está correlacionado con las variables explicativas. Si vemos en la tabla, hay errores positivos y negativos, es decir, el error es independiente de las horas de estudio. El contraejemplo sería este:
Acá hay una clara correlación creciente entre “X” y “u”: Hay una relación de dependencia, lo cual significa que estamos dejando información relevante dentro del error y, por lo tanto, el modelo no está bien planteado.
4 - No Colinealidad Perfecta (en Caso de Más de una Variable Explicativa)
Las variables explicativas no deben estar perfectamente correlacionadas entre sí.
Ejemplo: Supón que además de las horas de estudio, también usas como variable explicativa la cantidad de ejercicios resueltos. Estas dos variables no deben estar tan relacionadas que el modelo no pueda distinguir cuál de las dos está afectando realmente la calificación.
Contraejemplo: Si incluyes dos variables muy similares, como «horas de estudio» y «minutos de estudio», estas variables estarían tan correlacionadas que el modelo no podría diferenciar su impacto en la calificación, lo que sería un problema de colinealidad. Esto se llama multicolinealidad. Lo correcto es que no haya multicolinealidad. La forma más “fuerte” es como en este contraejemplo, en que utilizamos minutos y horas para predecir, siendo que las horas están compuestas por minutos. El coeficiente de Correlación de Pearson sería 100%.
No ahondaremos en fórmulas ya que no hemos visto regresiones con 2 o más variables explicativas.
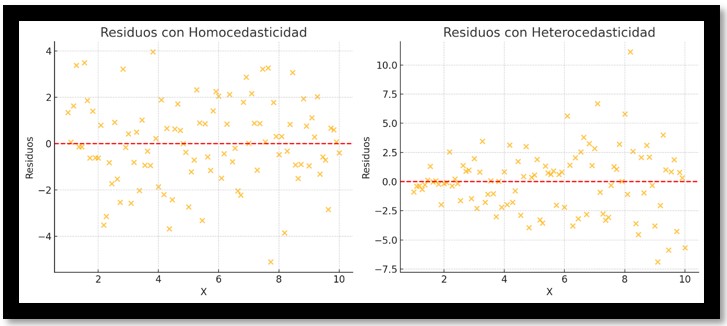
5 - Homocedasticidad
El supuesto de homocedasticidad dice que los errores deben tener una varianza constante para todos los valores de las variables explicativas.
Ejemplo: El error del modelo al predecir las calificaciones debería ser más o menos constante para todos los estudiantes, sin importar si estudiaron mucho o poco. Si un estudiante estudió 2 horas, el error de la predicción no debería ser sistemáticamente mayor o menor que para un estudiante que estudió 10 horas.
Contraejemplo: Si el modelo predice muy bien las calificaciones de estudiantes que estudian pocas horas, pero tiene grandes errores al predecir las calificaciones de aquellos que estudian muchas horas (por ejemplo, sobreestimando o subestimando más en estos casos), entonces estaríamos ante heteroscedasticidad.
La homocedasticidad se detecta bajo el test de Breusch-Pagan, que veremos a futuro.
Matemáticamente se escribe:
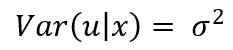
Esto quiere decir que “la varianza de cualquier “u” dada la de su respectivo “X”, debe ser un número constante”.
6 - No autocorrelación (para datos de series de tiempo)
Este supuesto es importante en los datos de series de tiempo (cuando tienes datos a lo largo del tiempo, como el crecimiento del PIB per cápita por año). Dice que los errores no deben estar relacionados en el tiempo.
Ejemplo: Si estás prediciendo las calificaciones de un mismo estudiante en varios exámenes durante el semestre, el error en la predicción de un examen no debería influir en el error del siguiente examen. Cada predicción debería ser independiente en el tiempo.
Contraejemplo: Si subestimas la calificación en el primer examen de un estudiante y luego también subestimas su calificación en los exámenes siguientes de manera consistente, los errores estarían correlacionados a lo largo del tiempo, lo que indica autocorrelación.
Por el momento, no hemos revisado series de tiempo.
7 - Normalidad de los errores (solo para inferencia)
Los errores deben distribuirse de manera normal, lo que significa que la mayoría de los errores deben ser pequeños, y los errores grandes deben ser raros.
Ejemplo: Si predices las calificaciones de varios estudiantes, la mayoría de las veces el error en la predicción debería ser pequeño, con solo algunos errores grandes. Estos errores deberían distribuirse en una forma de campana, donde los errores pequeños son los más comunes y los errores grandes son raros.
Contraejemplo: Si el modelo produce muchos errores grandes, tanto subestimando como sobreestimando las calificaciones, y estos errores no siguen una distribución normal, entonces los errores no serían normales, lo que podría afectar la validez de las inferencias del modelo.
Por el momento, al igual que arriba, tampoco hemos hecho inferencia todavía.
En resumen, estos supuestos aseguran que el modelo MCO sea válido y que los resultados sean interpretables de manera precisa. Si alguno de ellos no se cumple, el modelo puede tener problemas o producir resultados poco confiables. Pero falta un concepto.
Estimador MCO Insesgado / Concepto de Insesgadez
Si se cumple que el modelo es lineal en los parámetros (punto 1), el error tiene esperanza condicional cero dado X (punto 3) y no hay multicolinealidad (punto 4) estamos frente a MCO insesgados, esto quiere decir que:
Esto es una abstracción, significa lo siguiente: “En promedio (sobre infinitas muestras hipotéticas), el estimador «atinaría» al verdadero valor del parámetro.”
Es fundamental para hacer un buen estudio tener claros todos estos conceptos. Nótese que para la insesgadez no se requieren conceptos como la homocedasticidad, independencia entre observaciones y normalidad de los errores.