Como indicamos en entradas anteriores, esencialmente la econometría en su versión más simple es la estimación de la recta que más se asemeja a la línea de tendencia en un conjunto de datos. Esto presenta la particularidad que siempre existirá una línea de tendencia para estimar, aunque los datos estén muy dispersos y la relación no sea clara en lo absoluto.
Retomemos los datos y resultados ya obtenidos. El link de los datos los podrás descargar en el siguiente botón con los respectivos cálculos de esta entrada (es el mismo archivo de la entrada anterior).
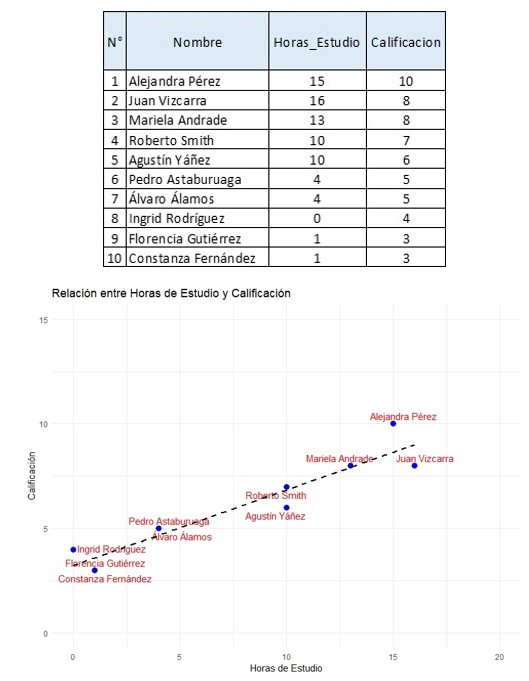
Llegamos a que la Ecuación de la Regresión Lineal Simple (Ecuación de la Recta) de la línea de tendencia es:
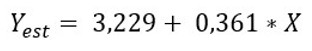
Es decir, que si una persona estudia X = 0 horas, obtiene un 3,229 de calificación estimada. La calificación Y = 10 se obtiene estudiando 18,76 horas (resultado de despejar 10 = 3,299 + 0,361*X).
Ahora, por sentido común sabemos que esto es una línea de tendencia y, por lo tanto, una mera aproximación a la realidad. Los puntos no están necesariamente sobre la recta. ¿Qué hubiese pasado si alguien hubiese obtenido la nota máxima con X = 0 horas de estudio?, ¿o si alguien hubiese obtenido la nota mínima con X = 15 horas de estudio? Que la recta sería más inexacta y especulativa. Los resultados dependerían quizás más del azar. El punto es que siempre encontraremos la ecuación de la regresión lineal simple.
Por lo tanto, corresponde analizar alguna forma de precisión del ajuste.
Test de Bondad de Ajuste
En estadística y econometría los test que miden la calidad de las estimaciones se llaman de “Bondad de Ajuste”, lo cual literalmente busca medir “qué tan bien se ajustan”. La fórmula matemática es:
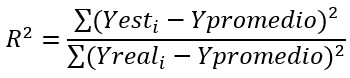
Se lee literalmente “R cuadrado” y su nombre real es “Coeficiente de Determinación”. Si resulta difícil de entender, no es más que lo siguiente:
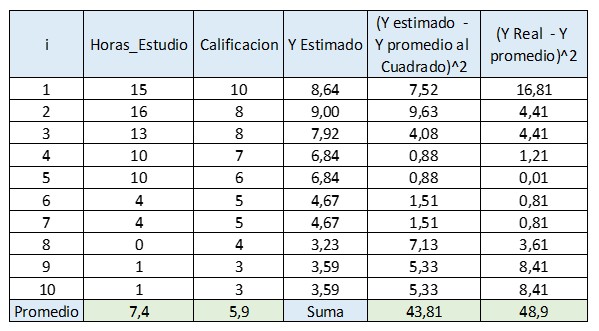
Para la primera estudiante Alejandra Pérez, sus horas de estudio fueron X = 15 y obtuvo una calificación de Y = 10. Utilizando sus X = 15 horas de estudio en la Regresión Lineal Simple obtenemos:
Y = 3,229 + 0,361*15 = 8,64
Este 8,64 es lo que corresponde a la recta de regresión lineal, por lo tanto, es su Calificación “Y estimada” (su calificación real fue más alta, por eso vemos su punto sobre la recta). A este número debemos restarle la calificación real promedio, es decir, el 5,9. Finalmente, ese resultado debemos elevarlo al cuadrado. Repitiendo el mismo cálculo para los otros 9 estudiantes y sumándolos, obtenemos 43,81, que es el numerador de la fórmula superior.
El denominador sigue la misma lógica pero con la calificación “Y” real.
Luego, el coeficiente de determinación o R cuadrado es 43,81/48,9 = 0,9.
Esto quiere decir que la recta estimada explica el 90% de la variación del resultado (hay una correlación positiva del 90% entre horas de estudio y calificación obtenida. Si el resultado fuera 1 significa que hay una correlación positiva perfecta y los puntos de horas de estudio y calificaciones reales estarían sobre la misma recta.
En este caso, al ser una regresión lineal simple, el R cuadrado o coeficiente de determinación también coincide con el “Coeficiente de Correlación de Pearson”.
La correlación sería menor si los puntos estuvieran más dispersos y no formarían una figura tan lineal, sino, por ejemplo, algo como esto:

El R cuadrado de cero resulta interesante, por cuanto los datos no correlacionan en absoluto, formando un círculo en el gráfico.
Por último, existe el R cuadrado ajustado, cuya fórmula es la siguiente:
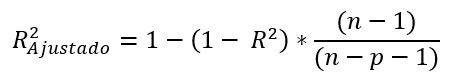
Se debe entender n como el número de alumnos, por lo tanto acá n = 10 y “p” es el número de variables que utilizamos para explicar el modelo, en este caso es sólo una (las horas de estudio) y por lo tanto tenemos p = 1.
Reemplazando, tenemos que el R cuadrado ajustado es 0,88 (lo podrás ver directo calculado en la fórmula del Excel).
La razón de la palabra “ajustado” es que es más estricto al castigar por el número de variables explicativas que utilizamos. En futuras publicaciones veremos lo que es una Regresión Lineal Múltiple, lo que corresponde a lo mismo que hemos hecho hasta ahora, pero con más variables explicativas. Es como si agregáramos a la tabla otra columna con la cantidad de ejercicios resueltos del tema evaluado. Como estamos intentado “apuntarle” a lo mismo, pero con más factores explicativos y datos, debemos ser más rigurosos a la hora de evaluar la regresión. En otras palabras, para el R cuadrado ajustado, menos es más: Si obtenemos dos regresiones con el mismo poder explicativo, nos indicará que debemos quedarnos con la que tiene menos variables explicativas.